在室内导航中,最优路径算法是一种非常重要的技术。它可以帮助用户在复杂的室内环境中找到从起点到终点的最佳路径。下面是关于室内导航算法中涉及的最优路径算法的一些信息。
一、最优路径算法原理
最优路径算法是一种广泛应用于各种领域,包括室内导航、交通网络、通信网络等的算法。其主要目标是,在给定的图中,找到从起点到终点的最短路径。这里的“最短”可以根据不同的度量标准来定义,例如距离、时间、成本等。
在室内导航的上下文中,最优路径算法需要考虑多种因素,包括但不限于:
距离:显然,用户通常希望找到最短的路径。这可以通过使用诸如Dijkstra的算法或A*搜索算法来实现。
方向:在某些情况下,用户可能更倾向于选择某些方向,例如,避免上下楼梯。最优路径算法可以纳入这样的偏好。
障碍物:室内环境通常充满了障碍物,如家具、墙壁等。路径规划算法需要考虑到这些障碍物,确保生成的路径是实际可行的。
实时信息:室内环境可能会随时间而变化,例如,某些路径可能因为临时的维修或活动而被封锁。最优路径算法需要能够处理这样的动态信息。

二、基于图论的最优路径算法的步骤
建图:将室内环境表示为图,其中节点代表可到达的位置(例如,房间的角落或门口),边代表可以通行的路径。
权重赋值:根据距离、方向、障碍物等因素,为图中的边赋权重。
路径搜索:使用诸如Dijkstra、A*或其他搜索算法来查找从起点到终点的最短路径。
优化与更新:根据用户的反馈和室内环境的变化,不断优化和更新图的结构和权重。
通过结合多种因素和算法优化,最优路径算法能够为室内导航提供高效、准确的解决方案。
三、最优路径算法种类
Dijkstra算法:这是一种非常著名的最短路径算法,适用于没有负权重的图。它从起点开始,逐步扩展到所有可达节点,并选择最短的路径。
A*算法:这是一种启发式搜索算法,使用一个评价函数来评估每个可能的路径。评价函数通常考虑目标的距离、到达目标的方向等因素。
Bellman-Ford算法:这是一种求解单源最短路径问题的算法。它适用于带有负权重的图,可以找到从起点到所有其他节点的最短路径。
Floyd-Warshall算法:这是一种求解所有节点对之间最短路径问题的算法。它适用于带有负权重的图,可以找到所有节点对之间的最短路径。

四、最优路径算法应用
最优路径算法在室内导航中有许多应用,例如:
商场导航:用户可以通过最优路径算法找到从起点到终点的最佳路径,避开障碍物和其他人流量大的区域。
机场导航:旅客可以使用最优路径算法找到从登机口到目的地的最佳路径,避免走错路或耽误时间。
博物馆导览:游客可以使用最优路径算法找到每个展品的位置,并规划最佳参观路线。
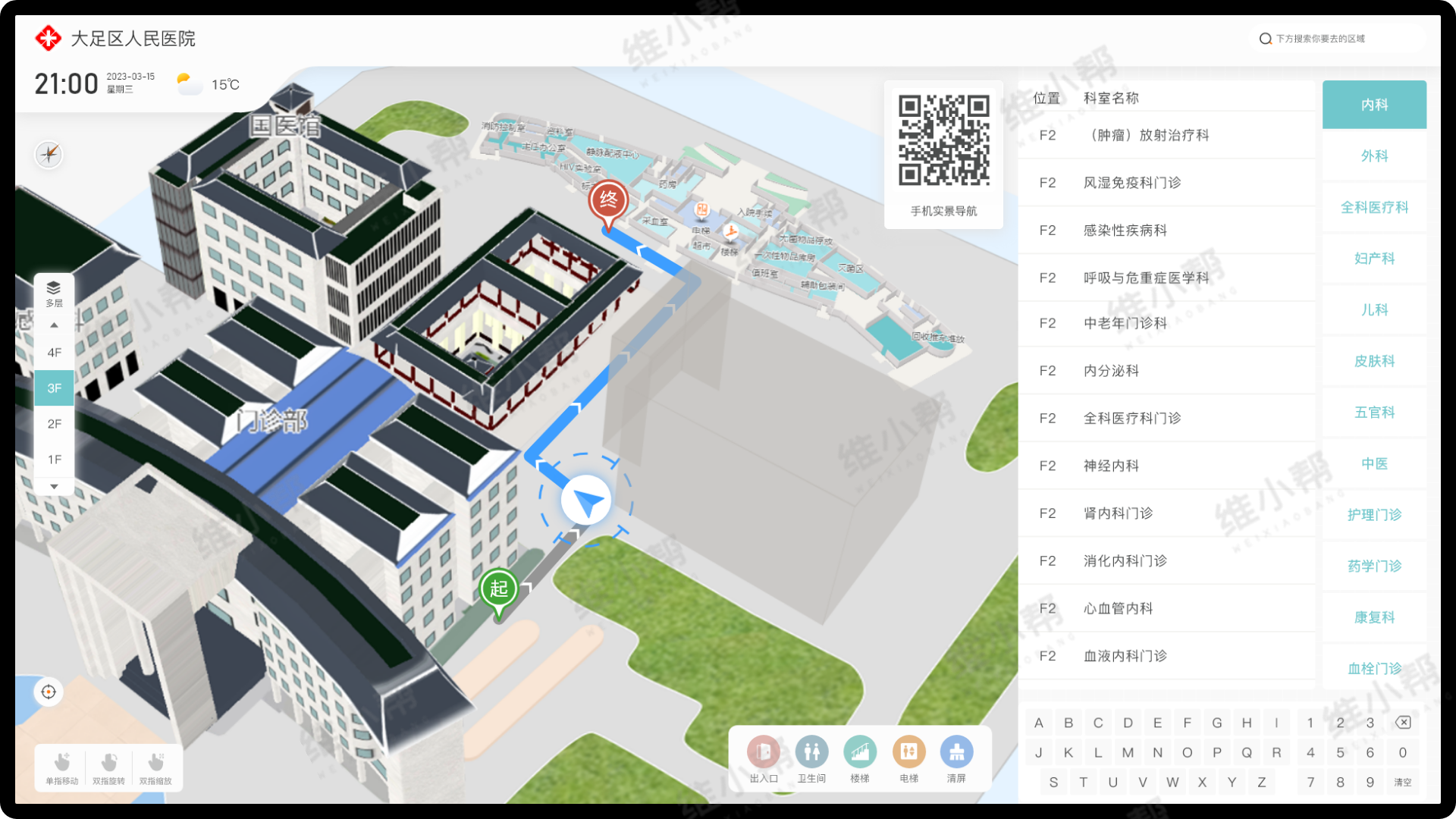
医院导航:病人和家属可以使用最优路径算法找到诊室、病房等目的地,减少在医院内部迷路的情况。

总之,最优路径算法是室内导航中非常重要的技术之一。除了上述提到的Dijkstra算法、A*算法、Bellman-Ford算法和Floyd-Warshall算法外,还有许多其他算法可以用于室内导航中。
下一篇:室内导航算法专题二-地图算法(图形算法)!






